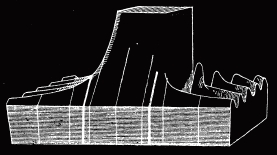
Elliptic integrals naturally arise when one wants to find the length of an elliptic arc (see, for example, the equations for the profile curve of an unduloid). Up to constants, this length is given by
$E(\varphi, k) = \int \limits_{0}^{\varphi} \sqrt{1 - k^2 \sin^2 \theta} d \theta$
an elliptic integral of the second kind.
Similar expression has an elliptic integral of the first kind
$u = F(\varphi, k) = \int \limits_{0}^{\varphi} \frac{1}{\sqrt{1 - k^2 \sin^2 \theta}} d \theta$.
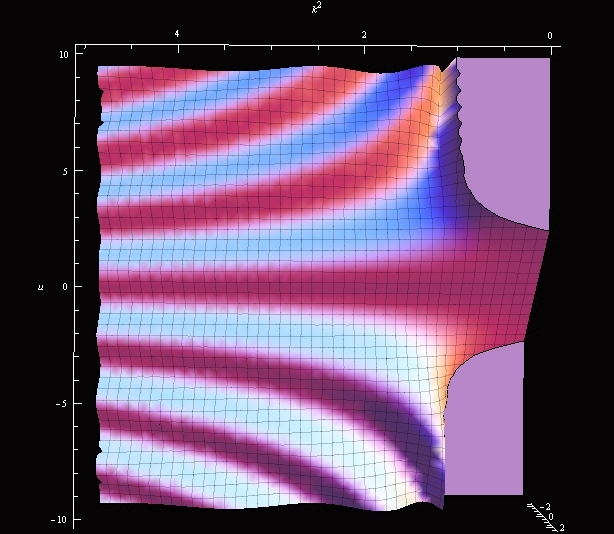
The model shows the graph of the Jacobi amplitude $\varphi = am(u,k)$ defined as the inverse w.r.t. $\varphi$ function $\varphi = F^{-1}(u, k)$.
Both elliptic integrals fall into a family of special functions, that is functions that cannot be expressed in terms of elementary functions (such as exponents, linear, trigonometric, logarithmic functions).
In most math software packages the Jacobi amplitude is a predefined special function. Below is an example in Mathematica (here $m=k^2$, and note that, unlike the plaster model, JacobiAmplitude[u,m] function in Mathematica is not symmetric w.r.t. the $m=0$ plane; see the source above)
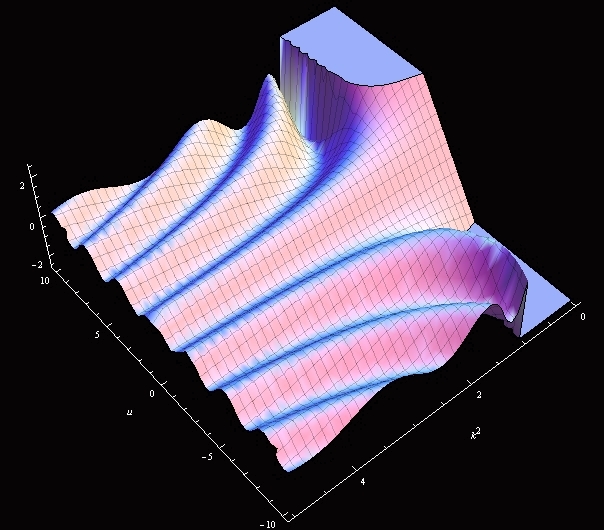
Observe that amplitude is an odd function w.r.t. $u$: