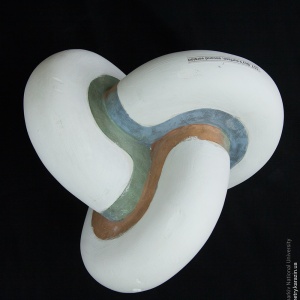
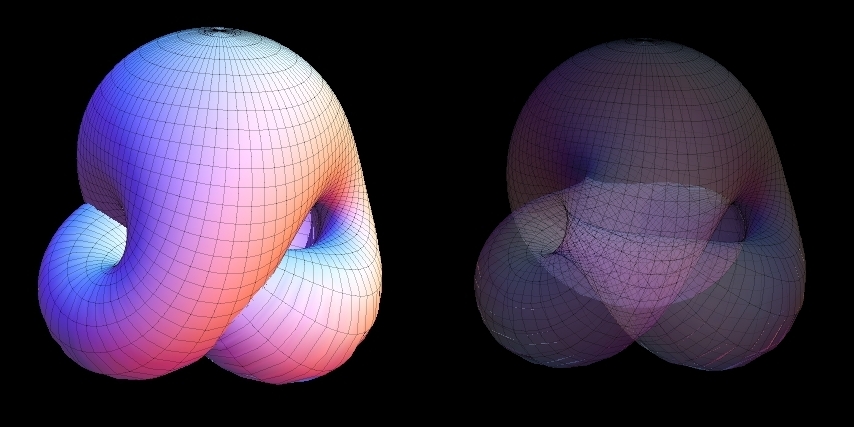Boy's surface has 3-fold symmetry. This means that it has an axis of discrete rotational symmetry: any 120° turn about this axis will leave the surface looking exactly the same. The Boy's surface can be cut into three mutually congruent pieces.
The line on the model depicts an orientation-reversing path, i.e. a closed loop on the surface such that if you start up-right (shown with an arrow) at one point and walk along the path once you will come to the starting point upside-down. This shows that a projective plane is non-orientable.
Boy's surface has self-intersections. Patches on the model painted in the same color are the parts of the surface that should be thought connected.
Boy's surface can be parametrized in the following way (discovered by Rob Kusner and Robert Bryant): given a complex number $w$ with $|w|\leqslant 1$, let
$g_1 = -{3 \over 2} \mathrm{Im} \left[ {w (1 - w^4) \over w^6 + \sqrt{5} w^3 - 1} \right],$
$g_2 = -{3 \over 2} \mathrm{Re} \left[ {w (1 + w^4) \over w^6 + \sqrt{5} w^3 - 1} \right],$
$g_3 = \mathrm{Im} \left[ {1 + w^6 \over w^6 + \sqrt{5} w^3 - 1} \right] - {1 \over 2},$
and the desired
Cartesian coordinates $x$, $y$, $z$ on Boy's surface are
$\begin{pmatrix}x\\ y\\ z\end{pmatrix} = \frac{1}{g_1^2 + g_2^2 + g_3^2} \begin{pmatrix}g_1\\ g_2\\ g_3\end{pmatrix}$
The result of the Mathematica code with the given above parametrization (see modeling for the source):