The animation below illustrates how the moving and rotating line generates a helicoid. This property makes a helicoid a ruled surface (of negative curvature):
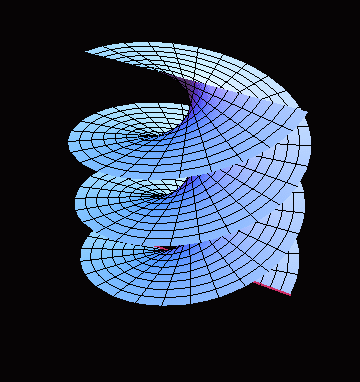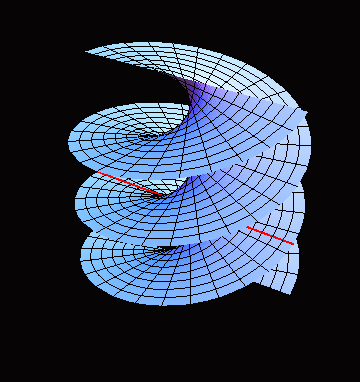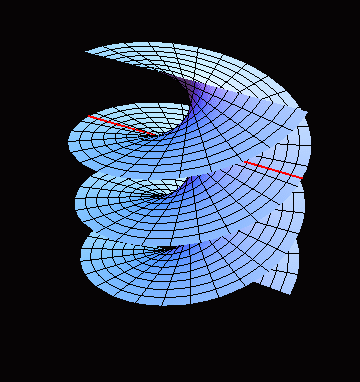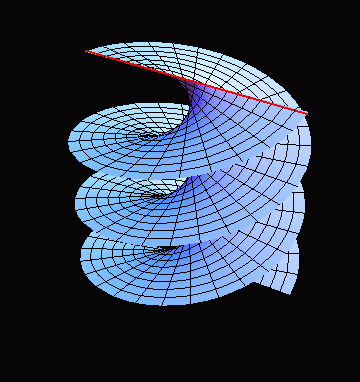
Helicoid is a minimal surface (i.e. its mean curvature $H=0$). The model shows the typical behaviour of lines of curvature and asymptotic lines on minimal surfaces. In particular, each asymptotic line of a minimal surface makes $\pi/4$ angle with a line of curvature it intersects.
Indeed, by the Euler formula for the normal curvature
$k_n = k_1 \cos^2 \varphi + k_2 \sin^2 \varphi$,
where $k_1$ and $k_2$ are principal curvatures, and $k_n$ is the normal curvature in the direction making the angle $\varphi$ with the first principal direction.
For minimal surfaces we have $H = (k_1 + k_2)/2 =0$, thus $k_1 = -k_2$, which, by plugging in the formula above, gives
$k_n = k_1 (\cos^2 \varphi - \sin^2 \varphi) = k_1 \cos 2\varphi$.
Therefore, for $\varphi = \pi/4$ we have a vanishing normal curvature, so by definition, $\varphi = \pi/4$ correspond to the asymptotic direction. This proves the claim.
In the parametrization above, each coordinate line is a line of curvature. For $v = const$ we have generating straight lines, for $u = const$ - helices.















